Co je doba trvání Macaulay?
Macaulay Duration je doba, kterou investor potřebuje, aby získal zpět své investované peníze do dluhopisu prostřednictvím kupónů a splácení jistiny. Tato doba je váženým průměrem období, kdy by měl investor zůstat investován do cenného papíru, aby se současná hodnota peněžních toků z investice shodovala s částkou zaplacenou za dluhopis.
Macaulayova doba trvání je velmi důležitým faktorem, který je třeba vzít v úvahu před nákupem dluhového nástroje. Může výrazně pomoci investorům vybrat si z různých sad cenných papírů s pevným výnosem na trhu. Jak všichni víme, ceny dluhopisů jsou nepřímo úměrné úrokovým sazbám. Investoři získají dobrý nápad, pokud jde o to, jaký dluhopis koupit, dlouhodobější nebo kratší, pokud znají dobu trvání, kterou různé kupónové dluhopisy nabízejí, spolu s předpokládanou strukturou úrokových sazeb.
Macaulayova doba trvání
Lze jej vypočítat pomocí následujícího vzorce,
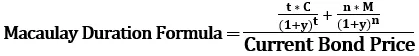

Kde,
- t = časové období
- C = platba kupónem
- y = výtěžek
- n = počet období
- M = splatnost
- Aktuální cena dluhopisu = současná hodnota peněžních toků
Výpočet doby trvání Macaulay s příkladem
Podívejme se na příklad Macaulayova trvání, abychom tomu lépe porozuměli.
Dluhopis v hodnotě 1 000 $ platí 8% kupónová sazba a je splatný za čtyři roky. Sazba kupónu je 8% pa S pololetní platbou. Můžeme očekávat, že nastanou následující peněžní toky.
- 6 měsíců: 40 $
- 1 rok: 40 USD
- 1,5 roku: 40 $
- 2 roky: 40 USD
- roky: 40 $
- 3 roky: 40 $
- 3,5 roku: 40 $
- 4 roky: 1040 USD
Vypočítejte dobu trvání Macaulay
Řešení:
S výše uvedenými informacemi můžeme vypočítat faktor slevy. K odvození diskontního faktoru můžeme použít následující pololetní úrokový vzorec. 1 / (1 + r) n, kde r je kupónová sazba, an je počet složených období.
Faktor slevy
Výpočet slevových faktorů po dobu 6 měsíců bude -

Faktory slevy po dobu 6 měsíců = 1 / (1 + 8% / 2)
Faktory slevy = 0,9615
Podobně můžeme provést výpočet diskontního faktoru pro roky 1 až 4.

Současná hodnota peněžních toků
Současná hodnota peněžního toku po dobu 6 měsíců bude -

Nyní, abychom získali aktuální hodnotu peněžních toků, musíme vynásobit peněžní tok každého období příslušným diskontním faktorem.
Současná hodnota peněžního toku po dobu 6 měsíců: 1 x 40 $ x 0,9615
Současná hodnota peněžního toku = 38,46 USD
Podobně můžeme provést výpočet současné hodnoty peněžních toků za 1. až 4. rok.

Macaulay trvání
Výpočet doby trvání Macaulay bude -

- Aktuální cena dluhopisu = PV všech peněžních toků 6 079,34
- Doba trvání Macaulay = 6 079,34 USD / 1 000 USD = 6,07934
Podrobný výpočet doby trvání Macaulay můžete zobrazit výše uvedenou šablonou aplikace Excel.
Přednosti použití doby trvání
Doba trvání hraje důležitou roli, protože pomáhá investorům pochopit rizikový faktor pro dostupné zajištění s pevným výnosem. Stejně jako se měří riziko v akciích odchylkou od průměru nebo jednoduše odvozením beta cenného papíru, riziko v nástrojích s pevným výnosem se striktně odhaduje podle Macaulayovy doby trvání nástroje.
Pochopení a porovnání Macaulayovy doby trvání nástrojů může při výběru vhodného pro vaše portfolio s pevným výnosem jít dlouhou cestu.
Nevýhody používání doby trvání
Doba trvání je dobrou aproximací cenových změn dluhopisů bez opcí, ale je dobrá pouze pro malé změny úrokových sazeb. Jak se změny úrokových sazeb zvětšují, zakřivení vztahu ceny dluhopisu k výnosu se stává důležitějším. Jinými slovy, lineární odhad cenových změn, jako je doba trvání, bude obsahovat chyby.
Ve skutečnosti není vztah mezi cenou dluhopisu a výnosem lineární, ale konvexní. Tato konvexnost ukazuje, že rozdíl mezi skutečnými a odhadovanými cenami se zvyšuje s růstem výnosů. To znamená, že rozšiřující se chyba v odhadované ceně je způsobena zakřivením skutečné cenové cesty. Toto se nazývá stupeň konvexnosti.
Sečteno a podtrženo
Znalosti o Macaulayově trvání jsou prvořadé při zjišťování budoucích výnosů z nástrojů s pevným příjmem. Proto je velmi vhodné, aby investoři, zejména investoři s averzí k riziku, posoudili a porovnali dobu trvání nabízenou různými dluhopisy, aby dosáhli minimální kombinace odchylek a dosáhli maximálních výnosů s co nejmenším rizikem. Před rozhodnutím o koupi je také třeba vzít v úvahu faktor úrokové sazby.








