Co je to korelační koeficient?
Korelační koeficient se používá k určení, jak silný je vztah mezi dvěma proměnnými a jeho hodnoty se mohou pohybovat od -1,0 do 1,0, kde -1,0 představuje negativní korelaci a +1,0 představuje pozitivní vztah. Zvažuje relativní pohyby proměnných a poté definuje, zda mezi nimi existuje nějaký vztah.
Vzorec koeficientu korelace
r = n (∑xy) - ∑x ∑y / √ (n * ( 2x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Kde
- r = korelační koeficient
- n = počet pozorování
- x = 1. proměnná v kontextu
- y = 2. proměnná
Vysvětlení
Pokud existuje nějaká korelace nebo řekněme vztah mezi dvěma proměnnými, pak to znamená, že pokud se jedna z proměnných změní v hodnotě, pak druhá proměnná bude mít také tendenci ke změně hodnoty, řekněme v konkrétní, která může být buď ve stejné nebo v opačným směrem. Čitatelská část rovnice provádí test a relativní sílu proměnných pohybujících se společně a jmenovatelská část rovnice škáluje čitatele vynásobením rozdílů proměnných od čtvercových proměnných.
Příklady
Příklad č. 1
Zvažte následující dvě proměnné, x a y, které musíte vypočítat korelační koeficient.
Níže jsou uvedeny údaje pro výpočet.

Řešení:
Pomocí výše uvedené rovnice můžeme vypočítat následující

Máme všechny hodnoty ve výše uvedené tabulce s n = 4.
Pojďme nyní zadat hodnoty pro výpočet korelačního koeficientu.

Výpočet je tedy následující,

r = (4 * 25 032,24) - (262,55 * 317,31) / √ ((4 * 20 855,74) - (262,55) 2 ) * ((4 * 30 058,55) - (317,31) 2 )
r = 16 820,21 / 16 831,57
Koeficient bude -

Koeficient = 0,99932640
Příklad č. 2
Země X je země s rostoucí ekonomikou a chce provést nezávislou analýzu rozhodnutí přijatých její centrální bankou ohledně změn úrokových sazeb, ať už měla vliv na inflaci a je schopna centrální banka kontrolovat.
Po shrnutí úrokové sazby a míry inflace, která v dané zemi v průměru za tyto roky převládala, jsou uvedeny níže.
Níže jsou uvedeny údaje pro výpočet.

Prezident země vás oslovil, abyste provedli analýzu a představili ji na příštím setkání. Použijte korelaci a určete, zda centrální banka splnila svůj cíl nebo ne.
Řešení:
Pomocí vzorce diskutovaného výše můžeme vypočítat korelační koeficient. Zacházení s úrokovou sazbou jako s jednou proměnnou, řekněme x, a s mírou inflace jako s jinou proměnnou jako s y.

Máme všechny hodnoty ve výše uvedené tabulce s n = 6.
Pojďme nyní zadat hodnoty pro výpočet korelačního koeficientu.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
Korelace bude -

Korelace = -0,92
Analýza: Ukazuje se, že korelace mezi úrokovou sazbou a mírou inflace je záporná, což se jeví jako správný vztah. Jak úroková sazba stoupá, inflace klesá, což znamená, že mají tendenci se pohybovat opačným směrem od sebe, a z výše uvedeného výsledku vyplývá, že centrální banka byla úspěšná při provádění rozhodnutí týkajícího se úrokové politiky.
Příklad č. 3
Laboratoř ABC provádí výzkum výšky a věku a chtěla vědět, zda mezi nimi existuje nějaký vztah. Shromáždili vzorek 1000 lidí pro každou z kategorií a přišli s průměrnou výškou v této skupině.
Níže jsou uvedeny údaje pro výpočet korelačního koeficientu.

Je od vás požadováno, abyste vypočítali korelační koeficient a dospěli k závěru, že pokud nějaký vztah existuje.
Řešení:
Zacházení s věkem jako s jednou proměnnou, řekněme x, a zacházení s výškou (v cms) jako s jinou proměnnou jako y.

Máme všechny hodnoty ve výše uvedené tabulce s n = 6.
Pojďme nyní zadat hodnoty pro výpočet korelačního koeficientu.

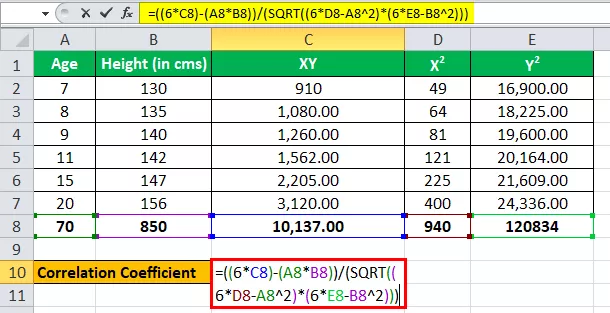
r = (6 * 10 137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20,834) - (850) 2 )
r = 1 322,00 / 1 361,23
Korelace bude -

Korelace = 0,971177099
Relevance a použití
Používá se ve statistice hlavně k analýze síly vztahu mezi proměnnými, které jsou v úvahu, a dále také měří, zda existuje nějaký lineární vztah mezi danými soubory dat a jak dobře by mohly být spojeny. Jedním z běžných opatření, která se používají při korelaci, je Pearsonův korelační koeficient.
Pokud se proměnná změní v hodnotě a spolu s touto další proměnnou se změní v hodnotě, pak je pochopení tohoto vztahu zásadní, protože lze použít hodnotu první proměnné k předpovědi změny hodnoty druhé proměnné. Korelace má dnes v této moderní době mnoho různých využití, například ve finančním průmyslu, ve vědeckém výzkumu a kde ne. Je však důležité vědět, že korelace má tři hlavní typy vztahů. První z nich je pozitivní vztah, který uvádí, že pokud dojde ke změně hodnoty proměnné, dojde ke změně související proměnné ve stejném směru. Podobně, pokud existuje negativní vztah, bude se příslušná proměnná chovat v opačném směru. Pokud také neexistuje žádná korelace, pak r bude znamenat nulovou hodnotu.Následující obrázky vám pomohou lépe porozumět konceptu.









