Složená definice
Složení je metoda výpočtu úrokové sazby, což je efektivní úrok z úroku, kde se úrok počítá z investice / počáteční jistiny plus vydělaného úroku a dalších reinvestic, jinými slovy vydělaný úrok se kumuluje k částce jistiny v závislosti na době vkladu nebo půjčky to může být měsíčně, čtvrtletně nebo ročně
Pokusme se pochopit, co se skládá a jak to funguje, na několika základních příkladech
Nejlepší 4 příklady síly složení
Příklad č. 1
Shane a Mark se rozhodli investovat 1 000 000 $, ale Shane se rozhodl investovat do jednoduchého úroku, zatímco Mark investuje do složeného úroku po dobu deseti let s 10% úrokem. Podívejme se, co se stane po deseti letech.
Řešení:
Výpočet Shaneovy investice tedy bude -

Celková částka výdělku = 200 000 $
S jednoduchým úrokem získá Shane po 10 letech 2 000 000 $.
Výpočet investice značky bude -

Celková částka výdělku = 2 59 374 USD
S úrokem Compound porostou investiční hodnoty Marka na 2 59 374 USD.
Nyní se Shane rozhodl investovat složením metod, jako je Mark, a oba investovali 2 000 000 USD ve výši 15%.
Výpočet Shaneovy investice bude -

Celková částka výdělku = 8,09 111,55 USD
Shane zůstává investován po dobu 10 let a získává konečnou částku 8,09 111,55 USD ve výši 15%.
Výpočet investice značky bude -

Celková částka výdělku = 65,83 790,52 $
Mark je však trpělivý dlouhodobý investor a zůstává investován 25 let a jeho investiční hodnota roste na 65,83 790,52 USD
Výše uvedený příklad ukazuje sílu složení. Čím delší je investiční horizont, tím větší je exponenciální růst.
Příklad č. 2 (týdně)
Simon má úspory ve výši 7500 dolarů a pro univerzitní fond svého syna, který se na vysokou školu bude účastnit po 15 letech, se rozhodl investovat do amerických spořicích dluhopisů. Simonovým cílem je ušetřit 20 000 $ a roční procentní sazba pro spořicí obligaci v USA je 6%. Jaká je budoucí hodnota Simon Money po 15 letech?
Řešení:
Vzhledem k tomu,
- Principal = 7500 $
- Sazba = 6% nebo 0,06
- Časové období = 15 let.
- Kolikrát je to složeno za rok n = 52 týdnů
- Budoucí hodnota =?
Výpočet budoucí hodnoty bude tedy -

Vzorec pro týdenní složení je uveden níže.
F = P (1 + r / n) n * t- F = 7500 $ (1 + 0,06 / 52) 52 * 15
- F = 7500 $ (1 + 0,001153846) 780
- F = 18 437,45 USD
Z výše uvedeného výpočtu je tedy zřejmé, že Simonova cíle ušetřit 20,00 $ výše uvedenými metodami nebude dosaženo, ale je tomu blíže.
Metoda spojitého skládání
Nyní zkusme výše uvedený příklad s Continuous Compounding Formula.
Výpočet budoucí hodnoty bude tedy -

- F = 7500 $ 0,06 * 15
- F = 7500 $ 0,9
- Budoucí hodnota (F) = 18 447,02 USD
Nyní ani při Continuous Compounding nebude Simonův cíl ušetřit 20 000 $ na univerzitní fond jeho syna.
Podívejme se s měsíčním složeným vzorcem na to, kolik peněz musel Simon investovat, aby dosáhl svého cíle ušetřit 20 000 $ za 15 let při RPSN 6%?
Výpočet budoucí hodnoty bude tedy -
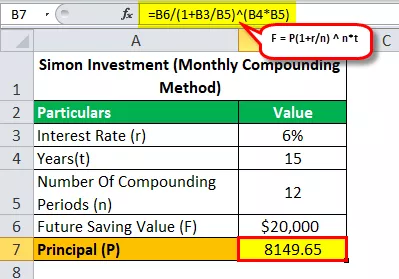
- 20 000 $ = P (1 + 0,06 / 12) 12 * 15
- P = 20 000 $ / (1 + 0,06 / 12) 12 * 15
- Principal (P) = 8149,65
Vyřešením výše uvedené rovnice tedy získáme odpověď ve výši 8 149,65 $ (částka, kterou musí Simon investovat, aby dosáhl svého cíle ušetřit 20 000 $ za 15 let).
Příklad č. 3 (efektivní roční výnos)
Řekněme, že omezená banka XYZ dává 10% ročně seniorům na fixní vklad a předpokládáme zde, že bankovní úroky jsou čtvrtletně složené jako všechny ostatní banky. Vypočítejte efektivní anualizovaný výnos za 5, 7 a 10 let.
Řešení:
Anualizovaný výnos po dobu 5 let:
- t = 5 let
- n = 4 (čtvrtletně složené)
- I = 10% ročně
Takže A = (1 + 10% / 100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1,6386
- I = 0,6386 za 5 let
Efektivní úrok = 0,6386 / 5
Efektivní I = 12,772% ročně
Anualizovaný výnos po dobu 7 let:
- t = 7 let
- n = 4 (čtvrtletně složené)
- I = 10% ročně
Takže A = (1 + 10% / 100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1,9965
- I = 1,9965 za 7 let
- Efektivní I = 0,9965/7
Efektivní I = 14 236% ročně
Anualizovaný výnos po dobu 10 let:
- t = 10 let
- n = 4 (čtvrtletně složené)
- I = 10% ročně
Takže A = (1 + 10% / 100/4) (10 * 4)
- A = (1 + 0,025) 40
- A = 2,685
- I = 1,685 za 10 let
- Efektivní I = 1,685 / 10
Efektivní I = 16,85% ročně
Příklad č. 4 - (Anuity: Budoucí hodnota)
1 000 $ se investuje každé 3 měsíce při 4,8% ročně, čtvrtletně. Kolik bude mít Annuity hodnotu za 10 let?
Řešení:
Takže když řekneme, kolik bude mít Anuita hodnotu za 10 let, znamená to, že zde musíme najít budoucí hodnotu, a to je důležité, protože kdykoli existuje příklad anuit, musíme vidět, co musíme zjistit.
Vzorec budoucí hodnoty tedy je
FV anuity = P ((1+ r) n - 1 / r)- P = Periodická platba
- r = sazba za období
- n = počet období
Vzorec budoucí hodnoty tedy je
- Takže tady P = 1 000 $
- r = 4,8% ročně nebo 0,048
- r (čtvrtletně) = 0,048 / 4
- r (čtvrtletně) = 0,012
- n = 10 let
- n (Kolikrát se použije složení) = 10 × 4 = 40
Výpočet FV anuity tedy bude -

Takže nyní FV = 1000 $ (1 + 0,012) 40 -1 / 0,012)
Takže řešením výše uvedené rovnice získá FV 50 955,30 $
Kolik tedy bude anuita za 10 let a odpověď je 50 955,30 $
Z výše uvedeného příkladu můžeme také zjistit, kolik úroků se získá za 10 let.
Protože 40krát je investováno 1 000 $, jedná se o celkovou investici (40 × 1 000 $ = 40 000 $).
Takže úrok = budoucí hodnota - celková investice
- Úrok = 50 955,30 USD - 40 000 USD
- Úrok = 10 955,30 USD
Tady je tedy důležité si uvědomit, že v anuitách mohou investoři získat velký zájem. Ve výše uvedených konkrétních příkladech dává vklad 40 000 $ na oplátku celkový úrok 10 955,30 $.
Poznámka: Pro podrobný výpočet si můžete stáhnout výše uvedenou šablonu aplikace Excel.








