Průměr a vážený průměr jsou v Excelu dva různé výrazy, průměr je metoda pro výpočet centrálního bodu daného souboru dat a počítá se tradičním způsobem výpočtu průměru sčítáním čísel dělených počtem přítomných souborů dat, zatímco vážený průměr je průměr, který se počítá stejným způsobem, ale s váhou vynásobenou každou sadou dat.
Rozdíl mezi průměrem a váženým průměrem
Průměrný vs. vážený průměr je matematický a statistický výraz ve financích a podnikání, ale oba se počítají odlišně. Průměr je součet všech jednotlivých pozorování dělený počtem pozorování. Průměr slouží k nalezení střední hodnoty v konkrétní sadě dat. To je také známé jako centrální tendence a používá se k nalezení centrální tendence skupiny dat v konkrétní skupině dat. Vážený průměr se používá v oblasti účetnictví. A jeho primárním účelem je najít správnou váhu nebo hodnotu, kterou je třeba vyřešit. Vážený průměr je hodnota splácení jistiny určitých dluhopisů nebo půjček, dokud není splacena hodnota jistiny.
Co je to průměr?
Průměr je součet všech jednotlivých pozorování dělený počtem pozorování. Používá se k nalezení střední hodnoty v konkrétní datové sadě. To je také známé jako centrální tendence a používá se k nalezení centrální tendence skupiny dat v konkrétní skupině dat. Používá se hlavně pro reprezentaci dat. Lze jej vyřešit pro sadu dat pomocí aritmetického vzorce.
Průměrný vzorec = součet pozorování / počet pozorování
Příklad průměru
Podívejme se na příklad, abychom pochopili průměr.
Předpokládejme, že ve třídě je deset studentů se známkami 50, 60, 70, 80, 65, 78, 95, 63, 58, 91, respektive ze 100. Nyní najdeme průměr výše známek studenta, jak ho známe.
Průměrný vzorec = součet pozorování / počet pozorování
Součet pozorování = 50 + 60 + 70 + 80 + 65 + 78 + 95 + 63 + 58 + 91
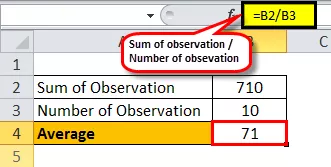
Průměr třídy 10 studentů je tedy 71.

Co je vážený průměr?
Vážený průměr se používá v oblasti účetnictví. Hlavním účelem je najít správnou váhu nebo hodnotu, kterou je třeba vyřešit. Vážený průměr je hodnota splácení jistiny určitých dluhopisů nebo půjček, dokud není splacena hodnota jistiny. Vážený průměr je také typem průměru s malým rozdílem, protože všechna pozorování nemají stejné váhy; odlišné pozorování má jinou důležitost; každé pozorování se vynásobí váhou a sečte. Váhový průměr se používá k provedení. Lze jej brát jako průměr, ve kterém má každá hodnota jinou váhu. A je ovlivněna váhou hodnoty dat. Vážená hodnota je součet produktu pozorování na hmotnost dělený součtem hmotnosti a lze ji zapsat jako: -
Vážený průměr vzorce = (a1w1 + a2w2 + a3w3 +… + anwn) / (w1 + w2 + w3… + wn)
Příklad váženého průměru
Podívejme se na příklad, abychom tomu lépe porozuměli.
Předpokládejme, že existují tři různé zkoušky, které přispívají k tomu, aby byly uděleny roční známky. U každé zkoušky je rozdílná váha pro první zkoušku váha 15%, pro druhou zkoušku váha 25% a pro závěrečnou zkoušku váha 60%. Předpokládejme, že student zaznamenal 60 známek v první zkoušce, 70 ve druhé a 80 v závěrečné zkoušce ze 100, nyní vypočítáme závěrečné známky studenta.
Pro výpočet použijte výše uvedený vzorec.
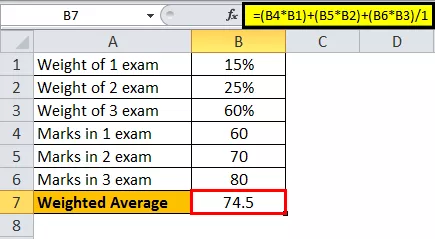
- Vážený průměr studenta je tedy 74,5.
Průměrná vs. vážená průměrná infografika
Zde vám poskytneme top 5 rozdílů.

Průměr vs Vážený průměr - klíčové rozdíly
Klíčové rozdíly mezi tímto průměrem jsou následující -
- Průměr je součet všech jednotlivých pozorování dělený počtem pozorování. Naproti tomu vážený průměr je pozorování vynásobené váhou a přidané k nalezení řešení.
- Průměr je matematická rovnice, zatímco vážený průměr se používá v každodenních činnostech financí.
- Průměr představuje reprezentaci souboru dat, zatímco vážený průměr je třeba vyhodnotit, aby se dospělo k řešení problému.
- Průměr lze vyřešit pro sadu dat pomocí aritmetického vzorce. Složce váženého průměru je dána váha hodnoty, aby se dospělo ke konkrétní odpovědi.
Průměrný vs vážený průměr Rozdíl mezi hlavami
Pojďme se nyní podívat na rozdíly mezi hlavami.
| Základ | Průměrný | Vážený průměr | ||
| Definice | Je to součet všech jednotlivých pozorování dělený počtem pozorování. | Je to pozorování vynásobené váhou a sečtené k nalezení řešení. | ||
| Rovnice | Je to matematická rovnice. | Uplatňuje se v každodenní činnosti financí. | ||
| Řešení | Jedná se o reprezentaci souboru dat. | Je třeba vyhodnotit, aby se dospělo k řešení problému. | ||
| Výpočty | Lze jej vyřešit pro sadu dat pomocí aritmetického vzorce. | Složce je přidělena váha hodnoty, aby se dospělo ke konkrétní odpovědi. |
Závěr
Takže jsme viděli průměr vs. vážený průměr a viděli jsme rozdíl mezi těmito dvěma. Viděli jsme, že průměr je součet všech jednotlivých pozorování dělený počtem pozorování a Průměr lze vyřešit pro sadu dat pomocí aritmetického vzorce, zatímco vážený průměr je pozorování vynásobené váhou a sečteno k nalezení řešení a složce váženého průměru je dána váha hodnoty, aby se dospělo ke konkrétní odpovědi. Oba mají různé uživatele založené na problému a oba jsou počítáni odlišně. Hlavním účelem váženého průměru je najít správnou váhu nebo hodnotu k řešení. Vážený průměr je průměrná hodnota splácení jistiny určitých dluhopisů nebo půjček, dokud není splacena hodnota jistiny. A průměr se používá k nalezení střední hodnoty nebo průměrné hodnoty.








